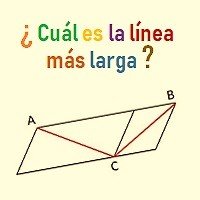
La Línea Más Larga de Sander y su Paralelogramo
En 1926 el psicólogo alemán Friedrich Sander describió una imagen basándose en un paralelogramo atravesado por dos líneas. La línea más larga de Sander y su paralelogramo consiste en identificar cuál de las dos líneas posee mayor longitud.
Si bien la imagen es conocida popularmente como el “Paralelogramo de Sander”, ya había sido publicada anteriormente por Matthew Luckiesh. Fue un investigador de los laboratorios de la compañía General Electric y en 1922 publicó un libro en el que aparecía el paralelogramo.
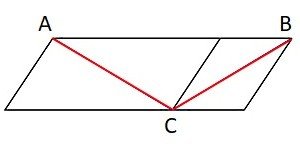
La representación gráfica es un paralelogramo dividido en dos partes, de tal manera que quedan construidos dos paralelogramos con diferentes tamaños. Ambos paralelogramos están atravesados por una línea, en este caso de color rojo, que conectan dos puntos.
¿Cuál es la línea más larga, la que conecta el punto A con el C o la que conecta el punto B con el C?. Antes de continuar leyendo este artículo te proponemos que observes el gráfico y des una respuesta.
Explicación de la Línea más larga de Sander
En verdad la pregunta es un poco engañosa, no hay una línea roja mas extensa que la otra, ambas líneas poseen la misma longitud. Por este motivo, el gráfico también es conocido con la ilusión óptica de Sander.
La línea diagonal del paralelogramos más grande, la que uno el punto A con el C, parece ser más larga que la línea que cruza el paralelogramo más pequeño. Y cuál es la explicación acerca de por qué percibimos visualmente que la línea que une el punto B con el C es más corta o menos extensa que la otra.
Una posible razón para explicar esta ilusión es que las líneas diagonales alrededor de las líneas oblicuas dan una percepción de profundidad similar al efecto de una perspectiva, y cuando las líneas diagonales forman parte de la representación virtual de esta profundidad, son percibidas como si tuvieran longitudes diferentes.






